La regla de Cramer es un teorema del álgebra
lineal que da la solución de un sistema lineal de ecuaciones en
términos de determinantes. Recibe este nombre en honor
a Gabriel
Cramer (1704 - 1752), quien publicó la regla en su Introduction à l'analyse des lignes courbes
algébriques de 1750, aunque Colin
Maclaurin también publicó el método en su Treatise of Geometry de 1748 (y
probablemente sabía del método desde 1729).
La regla de Cramer es de
importancia teórica porque da una expresión explícita para la solución del
sistema. Sin embargo, para sistemas de ecuaciones lineales de más de tres
ecuaciones su aplicación para la resolución del mismo resulta excesivamente
costosa: computacionalmente, es ineficiente para grandes matrices y por ello no
es usado en aplicaciones prácticas que pueden implicar muchas ecuaciones. Sin
embargo, como no es necesario pivotar matrices, es más eficiente que la eliminación gaussiana para matrices
pequeñas, particularmente cuando son usadas operaciones SIMD.
Ejemplo
La
resolución de un sistema de 2x2:
Dado:Regla_de_Cramer.

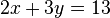
Que matricialmente
es:
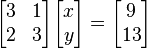
x , y pueden ser
resueltos usando la regla de Cramer
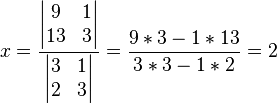
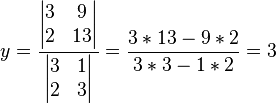
No hay comentarios:
Publicar un comentario