Matriz
cuadrada.
Se dice que una matriz A es
cuadrada si tiene el mismo número de filas que de columnas. Ejemplos de matriz
cuadrada:
Puede ser una matriz con valores

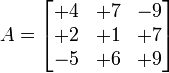
O también una matriz con subíndices (Genérica)


Puede ser de otro tamaño e incluso con variables
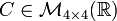

Se llama diagonal principal
de una matriz A a la diagonal formada por los elementos 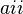 .
.
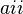 .
.
Se llama diagonal secundaria a la diagonal del cuadrado que no es la principal,
tiene por extremos los elementos  y
y 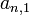 ,
como características, todos los elementos tienen la particularidad que sus
subíndices suman (n+1), por ejemplo
,
como características, todos los elementos tienen la particularidad que sus
subíndices suman (n+1), por ejemplo 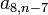 ,
donde 8 + (n - 7 ) = n + 1.
,
donde 8 + (n - 7 ) = n + 1.
 y
y 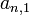 ,
como características, todos los elementos tienen la particularidad que sus
subíndices suman (n+1), por ejemplo
,
como características, todos los elementos tienen la particularidad que sus
subíndices suman (n+1), por ejemplo 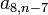 ,
donde 8 + (n - 7 ) = n + 1.
,
donde 8 + (n - 7 ) = n + 1.
Matriz
Rectangular.
Es aquella matriz que no es
cuadrada, esto es que la cantidad de filas es diferente de la cantidad de
columnas.
Puede ser de dos formas; vertical u horizontal.
Puede ser de dos formas; vertical u horizontal.
Matriz
Triangular superior.
Se dice que una matriz
(cuadrada) es triangular superior si todos los elementos que están por debajo
de la diagonal principal son nulos.
Matriz
Triangular inferior.
Se dice que una matriz es
triangular inferior si todos los elementos que están por encima de la diagonal
principal son ceros.
Matriz
Identidad.
Se llama matriz identidad de
orden n y se nota In a una matriz cuadrada de orden n en la que los elementos
de la diagonal principal son 1 y el resto 0.
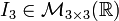
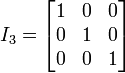
La matriz identidad puede ser de cualquier tamaño, siempre y cuando sea cuadrada.
Matriz
Traspuesta.
Matriz traspuesta (At). Se
llama matriz traspuesta de una matriz A a aquella matriz cuyas filas coinciden
con las columnas de A y las columnas coinciden con las filas de A.
- Para una matriz
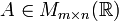 ,
se define la matriz transpuesta de
,
se define la matriz transpuesta de  ,
denotada por
,
denotada por 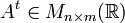 ,
como
,
como 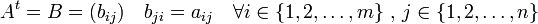 . Es decir, las filas
de la matriz
. Es decir, las filas
de la matriz  corresponden
a las columnas de
corresponden
a las columnas de  y
viceversa.
y
viceversa.
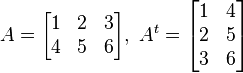
No hay comentarios:
Publicar un comentario