4.2.2 Operaciones con matrices (suma, diferencia, multiplicación por escalar y producto de matrices).

Suma de matrices.

Dadas dos matrices del mismo orden A y B, se llama matriz suma a la matriz que se obtiene de sumar los elementos correspondientes de A y B. Es decir el primer elemento de A con el primer elemento de B, el segundo de A con el segundo de B y así sucesivamente.

Es sencillo, pero si aún no lo entendiste fíjate en el ejemplo donde he marcado un elemento en cada matriz para que sea más evidente el procedimiento.

 

La matriz suma es del mismo orden que el de las matrices que se suman, por lo tanto estas dos deben ser del mismo orden.

Diferencia de matrices.

La suma de dos matrices A=(a_ij), B=(b_ij) de la misma dimensión, es otra matriz S=(s_ij) de la misma dimensión que los sumandos y con término genérico s_ij=a_ij+b_ij. Por tanto, para poder sumar dos matrices estas han de tener la misma dimensión.

La suma de las matrices A y B se denota por A+B.

Ejemplo:

Propiedades de la suma de matrices

1.   A + (B + C) = (A + B) + C (propiedad asociativa)

2.   A + B = B + A (propiedad conmutativa)

3.   A + 0 = A (0 es la matriz nula)

4.   La matriz –A, que se obtiene cambiando de signo todos los elementos de A, recibe el nombre de matriz opuesta de A, ya que A + (–A) = 0.

La diferencia de matrices A y B se representa por A–B, y se define como: A–B = A + (–B).

Multiplicación por escalar.

Si multiplicamos una matriz por una escalar, multiplicamos cada elemento de la matriz por ese escalar.

Es decir: producto de un número real por una matriz, es la aplicación que asocia a cada par formado por un número real y una matriz, otra matriz cuyos elementos se obtienen multiplicando el número real por todos los elementos de la matriz.

Ejemplo:

Sea  y 

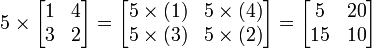
Producto de matrices.

En matemáticas, la multiplicación o producto de matrices es la operación de composición efectuada entre dos matrices, o bien la multiplicación entre una matriz y un escalar según unas determinadas reglas.

Al igual que la multiplicación aritmética, su definición es instrumental, es decir, viene dada por un algoritmo capaz de efectuarla. El algoritmo para la multiplicación matricial es diferente del que resuelve la multiplicación de dos números. La diferencia principal es que la multiplicación de matrices no cumple con la propiedad de conmutatividad.

Operaciones con matrices.