Matemáticas II: 4.3 Determinantes.

El determinante es como una forma multilineal alternada de un cuerpo. Esta definición indica una serie de propiedades matemáticas y generaliza el concepto de determinante haciéndolo aplicable en numerosos campos.

Métodos de cálculo.

Para el cálculo de determinantes de matrices de cualquier orden, existe una regla recursiva (teorema de Laplace) que reduce el cálculo a sumas y restas de varios determinantes de un orden inferior. Este proceso se puede repetir tantas veces como sea necesario hasta reducir el problema al cálculo de múltiples determinantes de orden tan pequeño como se quiera. Sabiendo que el determinante de un escalar es el propio escalar, es posible calcular el determinante de cualquier matriz aplicando dicho teorema.

Además de esta regla, para calcular determinantes de matrices de cualquier orden podemos usar otra definición de determinante conocida como Fórmula de Leibniz.

La fórmula de Leibniz para el determinante de una matriz cuadrada A de orden n es:

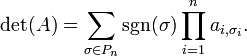
$\det(A) = \sum_{\sigma \in P_n} \sgn(\sigma) \prod_{i=1}^n a_{i,\sigma_i}.\$

Donde la suma se calcula sobre todas las permutaciones σ del conjunto {1,2,...,n}. La posición del elemento i después de la permutación σ se denota como σ_i. El conjunto de todas las permutaciones es P_n. Para cada σ, sgn(σ) es la signatura de σ, esto es +1 si la permutación es par y −1 si es impar (ver Paridad de permutaciones).

Matrices de orden inferior.

El caso de matrices de orden inferior (orden 1, 2 ó 3) es tan sencillo que su determinante se calcula con sencillas reglas conocidas. Dichas reglas son también deducibles del teorema de Laplace.

Una matriz de orden uno, es un caso trivial, pero lo trataremos para completar todos los casos. Una matriz de orden uno puede ser tratada como un escalar, pero aquí la consideraremos una matriz cuadrada de orden uno:

$A = \left [ \begin{array}{c} a_{11} \end{array} \right ]$

El valor del determinante es igual al único término de la matriz:

$\det A = \det \left [ \begin{array} {c} a_{11} \end{array} \right ] = \begin{vmatrix} a_{11} \end{vmatrix} = a_{11}$

El determinante de una matriz de orden 2:

$A = \left [ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right ]$

se calculan con la siguiente fórmula:

$| A | = \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} = a_{11} a_{22} - a_{12} a_{21}$

Dada una matriz de orden 3:

$A = \left [ \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right ]$

El determinante de una matriz de orden 3 se calcula mediante la regla de Sarrus:

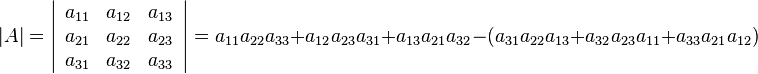
$|A| = \left | \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right | = a_{11} a_{22} a_{33} + a_{12} a_{23} a_{31} + a_{13} a_{21} a_{32} - (a_{31} a_{22} a_{13} + a_{32} a_{23} a_{11} + a_{33} a_{21} a_{12})$

Determinantes de orden superior.

El determinante de orden n, puede desarrollarse a partir de una fila o columna, reduciendo el problema al cálculo de un determinante de orden n-1. Para ello se toma una fila o columna cualquiera, multiplicando cada elemento por su cofactor (es decir, el determinante de la matriz que se obtiene eliminando la fila y columna correspondiente a dicho elemento, multiplicado por (-1)^i+j donde i es el número de fila y j el número de columna). La suma de todos los productos es igual al determinante.

La cantidad de operaciones aumenta muy rápidamente. En el peor de los casos (sin obtener ceros en filas y columnas), para un determinante de orden 4 se deberán desarrollar 4 determinantes de orden 3. En un determinante de orden 5, se obtienen 5 determinantes de orden 4 a desarrollar, dándonos 20 determinantes de orden 3. 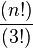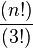El número de determinantes de orden 3 que se obtienen en el desarrollo de un determinante de orden n es igual a $(n!) \over (3!)$ .

Por ejemplo, mediante este método, para un determinante de orden 10 se deberán calcular 10 x 9 x 8 x 7 x 6 x 5 x 4 = 604.800 determinantes de orden 3.

También puede utilizarse el Método de eliminación Gaussiana, para convertir la matriz en una matriz triangular. Si bien el proceso puede parecer tedioso, estará muy lejos de los 14.529.715.200 de determinantes de orden 3 necesarios para calcular el determinante de una matriz de orden 14.

Determinante.

Matemáticas II

domingo, 22 de noviembre de 2015

4.3 Determinantes.

No hay comentarios:

Publicar un comentario