Es
un conjunto de ecuaciones lineales (es decir, un sistema de
ecuaciones en donde cada ecuación es de primer grado), definidas
sobre un cuerpo o un anillo conmutativo.
Introducción
En general, un sistema con m ecuaciones
lineales y n incógnitas puede ser escrito en forma normal
como:
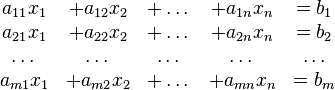
Donde  son
las incógnitas y los números
son
las incógnitas y los números 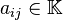 son
los coeficientes del sistema sobre el cuerpo
son
los coeficientes del sistema sobre el cuerpo![\mathbb{K}\ [= \R, \mathbb{C}, \dots]](https://upload.wikimedia.org/math/d/d/1/dd172d7f353ca18a891dda59a0d44cc5.png) . Es
posible reescribir el sistema separando con coeficientes con notación
matricial:
. Es
posible reescribir el sistema separando con coeficientes con notación
matricial:
 son
las incógnitas y los números
son
las incógnitas y los números 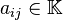 son
los coeficientes del sistema sobre el cuerpo
son
los coeficientes del sistema sobre el cuerpo![\mathbb{K}\ [= \R, \mathbb{C}, \dots]](https://upload.wikimedia.org/math/d/d/1/dd172d7f353ca18a891dda59a0d44cc5.png) . Es
posible reescribir el sistema separando con coeficientes con notación
matricial:
. Es
posible reescribir el sistema separando con coeficientes con notación
matricial: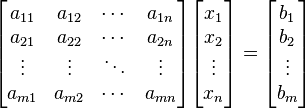
Si representamos cada matriz
con una única letra obtenemos:
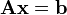
Donde A es
una matriz m por n, x es un
vector columna de longitud n y b es otro
vector columna de longitud m. El sistema de eliminación de
Gauss-Jordan se aplica a este tipo de sistemas, sea cual sea el cuerpo del
que provengan los coeficientes. La matriz A se llama matriz de coeficientes de este
sistema lineal. A b se le llama vector de términos
independientes del sistema y a x se le llama vector de
incógnitas.
Sistemas lineales reales
En esta sección se analizan
las propiedades de los sistemas de ecuaciones lineales sobre el cuerpo  , es decir, los
sistemas lineales en los cuales los coeficientes de las ecuaciones son números
reales.
, es decir, los
sistemas lineales en los cuales los coeficientes de las ecuaciones son números
reales.
 , es decir, los
sistemas lineales en los cuales los coeficientes de las ecuaciones son números
reales.
, es decir, los
sistemas lineales en los cuales los coeficientes de las ecuaciones son números
reales.
No hay comentarios:
Publicar un comentario