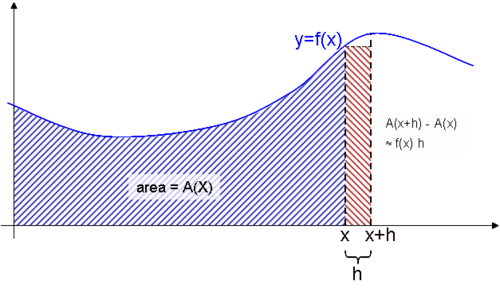
El teorema fundamental del cálculo consiste
(intuitivamente) en la afirmación de que la derivación e integración de
una función son operaciones inversas. Esto significa que toda función
acotada e integrable (siendo continua o discontinua en un número finito de
puntos) verifica que la derivada de su integral es igual a ella misma. Este
teorema es central en la rama de las matemáticas denominada análisis
matemático o cálculo.
El teorema es fundamental
porque hasta entonces el cálculo aproximado de áreas -integrales- en el que se
venía trabajando desde Arquímedes, era una rama de las matemáticas que se
seguía por separado al cálculo diferencial que se venía desarrollando por Isaac
Newton, Isaac Barrow y Gottfried Leibniz en el siglo
XVIII y dio lugar a conceptos como el de las derivadas. Las integrales
eran investigadas como formas de estudiar áreas y volúmenes,
hasta que en ese punto de la historia ambas ramas convergieron, al demostrarse
que el estudio del "área bajo una función" estaba íntimamente
vinculado al cálculo diferencial, resultando la integración, la operación
inversa a la derivación.
Una consecuencia directa de
este teorema es la regla de Barrow, denominada en ocasiones segundo teorema fundamental del cálculo,
y que permite calcular la integral de una función utilizando la integral
indefinida de la función al ser integrada.
No hay comentarios:
Publicar un comentario