2.3.5 Integral de una constante por una función de x.

 En cálculo, la integral indefinida de una función dada (es decir, el conjunto de todas las primitivas de la función) se escribe siempre con una constante, la constante de integración. Esta constante expresa una ambigüedad inherente a la construcción de primitivas. Si una función f está definida en un intervalo y F es una primitiva de f, entonces el conjunto de todas las primitivas de f viene dado por las funciones F (x) + C, siendo C, una constante arbitraria.

Origen de la constante.

La derivada de cualquier función constante es cero. Una vez se ha encontrado una primitiva F, sumándole o restándole una constante C se obtiene otra primitiva, porque (F + C) ' = F ' + C ' = F'. La constante es una manera de expresar que cada función tiene un número infinito de primitivas diferentes.

Por ejemplo, supóngase que se quiere encontrar las primitivas de cos(x). Una de estas primitivas es sin(x). Otra es sin(x)+1. Una tercera es sin(x)-π. Cada una de estas funciones tiene por derivada cos(x), por lo tanto todas son primitivas de cos(x). Resulta que añadir y restar constantes es el único grado de libertad que hay al encontrar primitivas diferentes de la misma función. Es decir, todas las primitivas son las mismas con la diferencia de una constante. Para expresar este hecho para cos(x), se escribe:

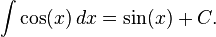
Sustituyendo C por un número cualquiera, se obtiene una primitiva. En cambio, escribiendo C en vez de un número se obtiene una descripción compacta de todas las primitivas posibles de cos(x). C se denomina constante de integración. Se puede comprobar fácilmente que todas estas funciones son, en efecto, primitivas de cos(x):

Constante_de_integración.