4.1.5.1 Definición de matriz.

En matemáticas, una matriz es un arreglo bidimensional de números. Dado que puede definirse tanto la suma como el producto de matrices, en mayor generalidad se dice que son elementos de un anillo. La notación de una matriz  tiene la forma: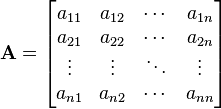

Las matrices se utilizan para múltiples aplicaciones y sirven, en particular, para representar los coeficientes de los sistemas de ecuaciones lineales o para representar transformaciones lineales dadas una base. En este último caso, las matrices desempeñan el mismo papel que los datos de un vector para las aplicaciones lineales.

Pueden sumarse, multiplicarse y descomponerse de varias formas, lo que también las hace un concepto clave en el campo del álgebra lineal.

Matriz.