1.2 Derivadas parciales.

En matemáticas, una derivada parcial de una función de diversas variables, es su derivada respecto a una de esas variables manteniendo las otras como constantes. Las derivadas parciales son útiles en cálculo vectorial y geometría diferencial.

La derivada parcial de una función f respecto a la variable x se representa con cualquiera de las siguientes notaciones equivalentes:

Donde  es la letra 'd' redondeada, conocida como la 'd de Jacobi'.

Cuando una magnitud  es función de diversas variables (x, y, z), es decir:

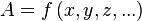
Al realizar esta derivada obtenemos la expresión que nos permite obtener la pendiente de la recta tangente a dicha función  en un punto dado. Esta recta es paralela al plano formado por el eje de la incógnita respecto a la cual se ha hecho la derivada y el eje z.

Analíticamente el gradiente de una función es la máxima pendiente de dicha función en la dirección que se elija. Mientras visto desde el álgebra lineal, la dirección del gradiente nos indica hacia donde hay mayor variación en la función.

Introducción

Supongamos que  es una función de más de una variable, es decir una función real de variable vectorial. Para el caso;

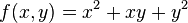
Un gráfico de z = x² + xy + y². Queremos encontrar la derivada parcial en (1, 1, 3) que deja a y constante; la correspondiente línea tangente es paralela al eje x.

Es difícil describir la derivada de tal función, ya que existe un número infinito de líneas tangentes en cada punto de su superficie. La derivación parcial es el acto de elegir una de esas líneas y encontrar su pendiente. Generalmente, las líneas que más interesan son aquellas que son paralelas al eje x, y aquellas que son paralelas al eje y.

Este es un corte del gráfico de la derecha donde y = 1.

Una buena manera de encontrar los valores para esas líneas paralelas es la de tratar las otras variables como constantes mientras se deja a variar sólo una. Por ejemplo, para encontrar la línea tangente de la función de arriba en (1, 1, 3) que es paralela el eje x, tratamos a la variable y como constante. El gráfico de la función y el plano y = 1 se muestran a la derecha. A la izquierda, vemos cómo se ve la función, en el plano y = 1. Encontrando la línea tangente en este gráfico, descubrimos que la pendiente de la línea tangente de ƒ en (1, 1, 3) que es paralela al eje x es tres. Que escribimos:

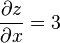
en el punto (1, 1, 3), o como "La derivada parcial de z con respecto a x en (1, 1, 3) es 3."

Derivada_parcial.