En el área de Análisis
Matemático, la integral de Riemann, es una forma de abordar el problema de la integración de
funciones. La integral de Riemann de una función real de variable real se
denota usualmente de la siguiente forma:
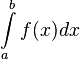
Si bien el artículo en gran
parte se restringe a la integración sobre intervalos acotados de![\scriptstyle [a,b] \subset \R^1](https://upload.wikimedia.org/math/b/2/8/b280156de276f39cd30db16666678c7a.png)
, el
concepto puede generalizarse a dominios acotados de 
sin
mucha dificultad.
, el
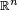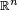concepto puede generalizarse a dominios acotados de sin
mucha dificultad.
Definición formal.
Se van a definir cuatro
conceptos, el último siendo el que nos interesa: el primero una partición de un intervalo [a, b],
el segundo la norma de una partición, el tercero una suma de Riemann y el
último que una función acotada sea Riemann integrable en un intervalo [a,b].
Partición de un intervalo y
su norma.
Sea [a,b] un intervalo
cerrado sobre los números reales. Entonces una partición de [a,b]
es un subconjunto finito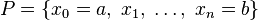 
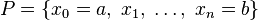tal
que xi > xi - 1, con i = 1,...,n. La
norma de la partición es el intervalo más grande:
tal
que xi > xi - 1, con i = 1,...,n. La
norma de la partición es el intervalo más grande:
Lo que estamos haciendo en
pocas palabras es cortar al intervalo en subintervalos disjuntos, cuya unión
forma el intervalo original, la norma es el valor del
intervalo de mayor longitud.
No hay comentarios:
Publicar un comentario